Game theory is an interactive decision theory; thus it’s a study of games. You can look at many real-life interactions as games. Football, soccer, and baseball games are some of the examples of games. So are the duopolistic interactions, the pre-election political campaigns between parties, and the interactions between the armed forces and nations. Even some interactions in nature between animal or plant species can be considered as games. In fact, in recent decades, game theory has been used in many different areas, including economics, political science, psychology, sociology, computer science and biology. Below are some of the cases in regard of four types of game theory.
1. The Battle of the Sexes
Many games are hard to solve as prisoners’ dilemmas. Thus, the players don’t have dominant strategies despite being in most strategic situations. What each player needs to do will usually depend on what the other players do. The Battle of Sexes was studied by R. Duncan Luce and Howard Raiffa, in the book of Game and Decisions: Introduction and Critical Survey. It is often expressed as a game between a man and a woman. Both the man and the woman are better off by cooperating and/or coordinating their activities. The man has a preference for one activity and the woman has preference for another activity but they would both prefer to do any activity together as they value each other’s company. Thus, it can be explained as a matrix below along with the scores:
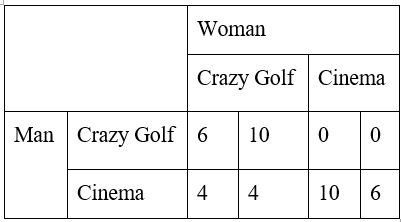
From the matrix above, we can see that the man prefers going to the cinema than playing crazy golf. We can also see that the woman prefers playing crazy golf than going to the cinema. The matrix also tells us that the man and the woman get more enjoyment from doing an activity together either playing crazy golf or going to the cinema than doing a favorite activity by themselves.
The Nash equilibrium for this case, as for man, the biggest value on his row is 6 which from playing the crazy golf together with the woman and from watching the cinema also together with the woman with a value of 10. Next, for the woman, the biggest value on her column is 10 which is from playing the crazy golf together with the man and from watching the cinema also together with the man with a value of 6. Thus, the Nash equilibrium is the matrix value that both have the biggest value from man and woman, which when both the man and women watching together either the cinema or play the crazy golf.
2. Leader Game
It was a long wait that the next generation of listening devices that gadget company would produce next, was the wireless earphones. It was just a matter of time and people wondering who was going to launch it first. There were some consideration for launching the product by the two market leaders of smartphones -Apple and Samsung.

The condition was if Apple and Samsung launch the wireless earphones at the same time, the market portion of this product would be divided and thus both of the companies could not get the best out of profit, although it was still producing some profits. However, if one of the two companies launched their product first, it would get the best profit from the market since they would be the market leader. While the first company would be the market leader, if the other company decided not to launch, they surely could not get the greatest profit.
However, since they would launch sometimes after the first company, they would also get profits. Let us just take an example that has happened before, which was when Apple launched their AirPods first than the Galaxy Buds from Samsung. Although Samsung’s profit would not be higher than Apple, Samsung could get profit that was higher than when they launched together. It was because when Samsung decided not to launch, they would surely launch some other time after Apple launched it.
When the time comes, the market would be ready to accept new product, whether as for alternatives from Apple AirPods or for the customers that wait to buy the best wireless earphone. The sales for Samsung would not before would also not drastically lower than Apple, since they have their own fans. The last condition is if both Apple and Samsung decide not to launch their product. Yes, they would not get any profit directly, but by not releasing it soon they both could keep the market curious and pay attention.
The Nash equilibrium for this case, as for Apple, the biggest value on its row is 4 which by launching the product while Samsung did not. Another biggest value in its row is by not launching the product while Samsung launched it with a value of 3. Next, for Samsung, the biggest value on its column is 4 which by launching the product while Apple did not. Another biggest value in its column is by not launching the product while Apple launched it with a value of 3. Thus, the Nash equilibrium is the matrix value when both have the biggest value from Apple and Samsung, which when either Apple and Samsung did the launching while the others did not.
3. Chicken Game
Chicken Game is a game that depict two drivers driving at high speeds towards each other. Each player can either drive straight or swerve. If one’s not having the courage to drive straight, the first to swerve would be called “chicken’’ and the other would be the winner. If no one swerves, both would suffer injuries or even die as a result of a fatal crash. If both drivers “chicken out”, they would drive in the opposite direction, which does not lead to an accident. (Madani and Hipel 2011 in Serrano 2011).
Therefore, we would like to explain one of the examples of the Chicken game which can be applied in the work environment. The subjects of this situation are workers and the management. The workers might be unhappy because of unsatisfactory working conditions, lack of pay increases or even pay cuts. They are most likely to collectively negotiate with management. The workers must decide if they want to accept what management is offering. Management must decide if they want to meet the demands of the workers. These decisions can be analyzed using the normal form game as shown below.
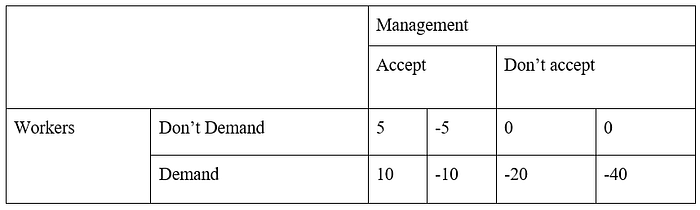
The matrix shows that if an agreement is reached (don’t demand, accept), the workers can benefit a little and there is a small cost to the company of meeting these demands. The matrix shows if workers demand more than what management offers and management agree (demand, accept), the workers benefit more and there is a larger cost to the company. The matrix shows if management does not accept any of the workers’ demands and the workers do not pursue any further (don’t demand, don’t accept), workers do not benefit and there are no extra costs to the company. The matrix shows if management do not agree to the workers terms and the workers wish to pursue their demands further by striking (demand, don’t accept).
Let’s assume an agreement has not been reached between workers and management of the company. Therefore, the workers rally together and refuse to work. While they are not working, they are not getting paid. While they are not working, the company that employs them is not earning revenue.
The Nash equilibrium for this case, as for workers, the biggest value on its row is 5 which by do not demand while the management accepts. Another biggest value in its row is by doing the demand, while the management accepts it, with a value of 10. Next, for management, the biggest value on its column is 5 which by accepting the demand while the workers demand it. Another biggest value in its column is by not accepting the demand while the workers do not demand, with a value of 0. Thus, the Nash equilibrium is the matrix value when both have the biggest value from workers and management, which when the management accept both when the worker demand and do not demand their offer.
4. Prisoner’s Dilemma
A prisoner’s dilemma is the most well-known type in game theory. Merrill M. Flood and Melvin Dresher of RAND Corporation were the one who developed the theory. The theory was depicting police arresting two guys and cannot convict them yet because there’s not enough evidence. Therefore, in order to deal with each of them, the interrogator offers: you’re allowed to be set free and other will be imprisoned for three years if you testify that the other is guilty; if two of them testify, both will be imprisoned for two years. Both will serve one year in prison, if the two of them keep their mouth shut.
Reflecting the case of Burger King versus McDonald, one of the companies decides to cut the price of their cheese burger. By doing so, the opposites don’t have no choice to follow the former in order to retain its profit. This will cause a slight increase for both companies. Thus, another condition is if Burger King decides to drop its price, while McDonald keeps the price higher. In this case, Burger King may win market share and earn more profits than McDonald.

The Nash equilibrium for this case, as for McDonald, the biggest profit on its row is 500 which when both McDonald and Burger King are increasing the price. Another biggest value in its row is by reducing the price, while Burger King increases the price, with a value of 700. Next, for Burger King, the biggest value on its column is 500 which when both McDonald and Burger King are increasing the price. Another biggest value in its column is by reducing the price, while McDonald increases the price, with a value of 750. Thus, the Nash equilibrium is the matrix value when both have the biggest value from McDonald and Burger King, which when both McDonald and Burger King increase the price.
—
This writing is used as one of the assignments in Strategic Decision Making and Negotiation class that I took at 2020. Credits to Adia, Cening, and Rafika as the writers of this assignment.
Reference:
https://steemit.com/economics/@spectrumecons/game-theory-4-battle-of-the-sexes seen on February 17th 2020
https://steemit.com/economics/@spectrumecons/game-theory-3-chicken-game seen on February 17th 2020
http://iilj.org/wp-content/uploads/2016/08/Serrano-etal-Game-Theory-2010.pdf seen on February 18th 2020
https://link.springer.com/content/pdf/10.1007/s40092-015-0120-z.pdf seen on February 18th 2020
https://www.researchgate.net/publication/277198987_Prisoner's_Dilemma_A_Case_Study seen on February 18th 2020